Naiara Korta Martiartu | USCT

Ultrasound computed tomography (USCT) is an emerging technique to image acoustic tissue properties. Originally, USCT scanning systems were developed for early breast cancer detection. They consist of a water tank in which the patient submerges the breast. The sidewalls of the water tank are equipped with ultrasound transducers that emit and record ultrasonic waves propagating through the tissue.

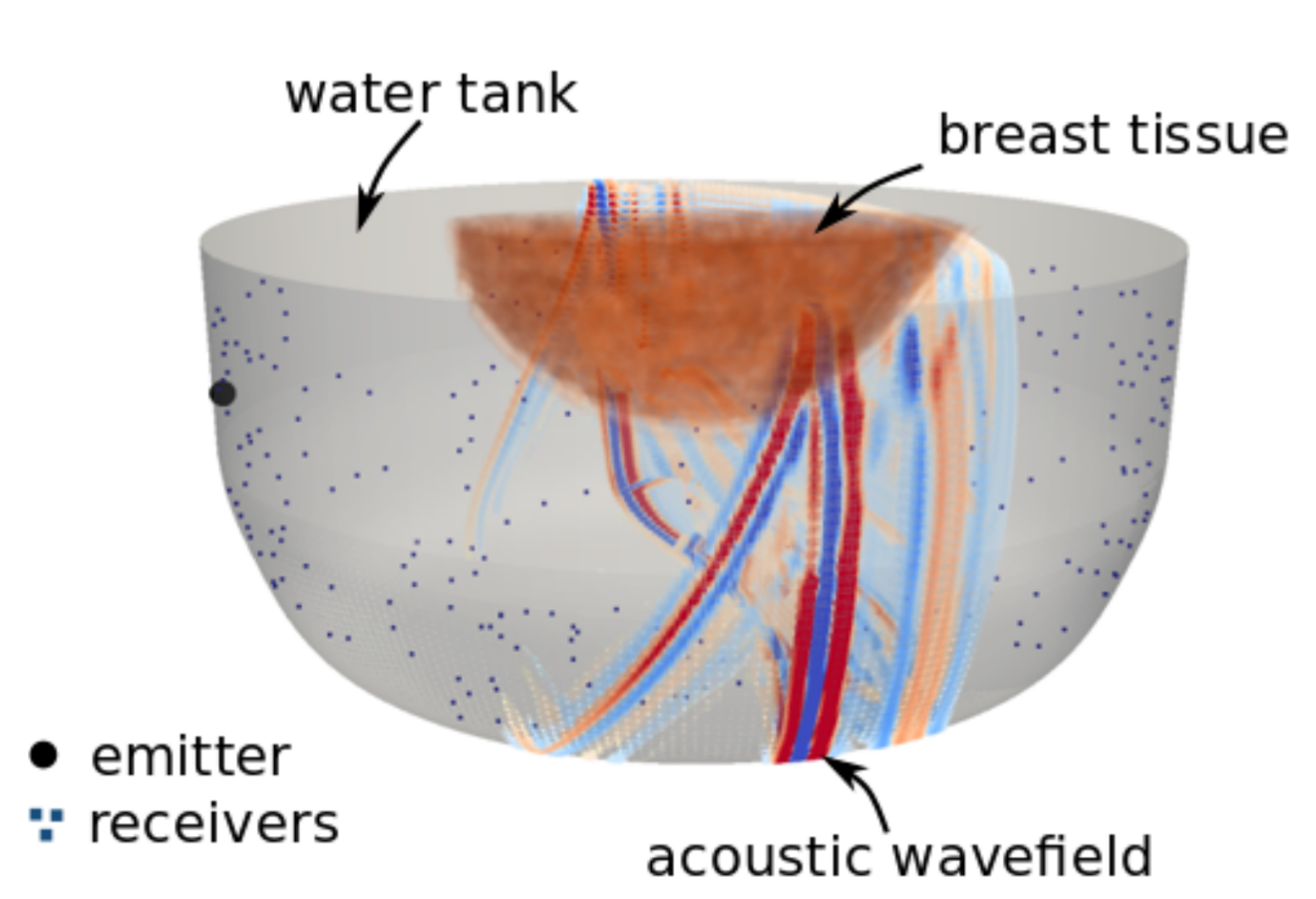
Ultrasound wave propagation through breast tissue using a 3D USCT device. This numerical example uses one transducer as emitter.

USCT is able to record both reflected and transmitted waves, which are essential to provide high-resolution quantitative images comparable to MRI. This is a significant improvement compared to traditional sonography techniques, where the gray-scale images are mainly qualitative. Quantitative images allow radiologists to discriminate between different tissue types and diagnose lesions more objectively.

My work on USCT has been focused on transferring knowledge from seismology to medical imaging in order to improve currect acquisition setups and tomographic algorithms. More details can be found in my Ph.D. thesis.

Finite-frequency tomography

Typical devices include high-frequency transducers, which makes tomography techniques based on numerical wave propagation simulations computationally challenging, especially in 3D. Therefore, despite the finite-frequency nature of ultrasonic waves, ray-theoretical approaches to transmission tomography are still widely used. In this work, we have introduced finite-frequency traveltime tomography to medical ultrasound. In addition to being computationally tractable for 3D imaging at high frequencies, the method has two main advantages:

(1) It correctly accounts for the frequency dependence and volumetric sensitivity of traveltime measurements, which are related to off-ray-path scattering and diffraction.

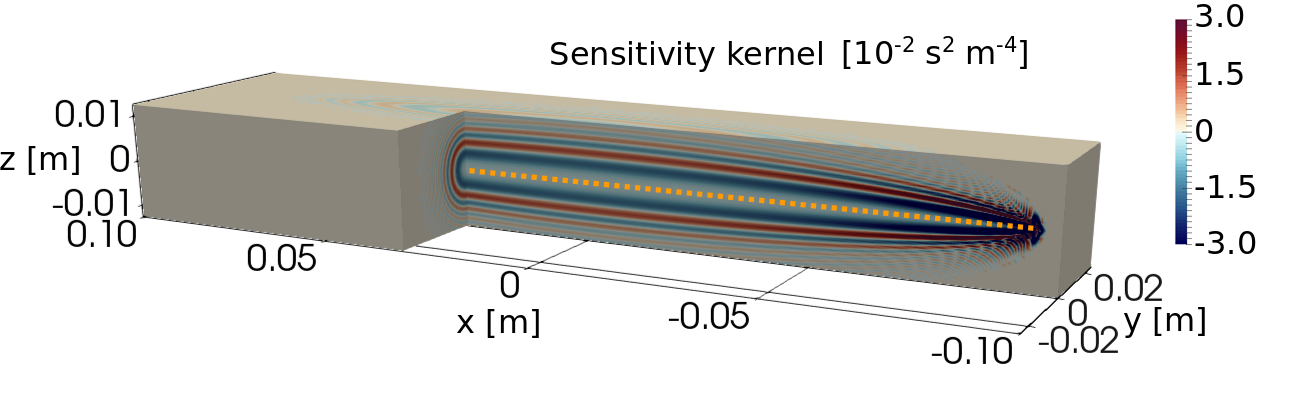
Example of sensitivity of finite-frequency traveltimes. It corresponds to a band-limited signal with frequencies in the range of 1–3 MHz. The emitter and the receiver are located at positions (-95,0,0) mm and (95,0,0) mm, respectively. The dashed line indicates the corresponding sensitivity predicted from ray theory.

(2) It naturally enables out-of-plane imaging and the construction of 3D images from 2D slice-by-slice acquisition systems.

3D velocity reconstruction using the dataset provided by the Spanish National Research Council (CSIC) and the Complutense University of Madrid (UCM) as part of the SPIE USCT Data Challenge 2017. We simulate a slice-by-slice acquisition, and we assume that the same data have been recorded at different elevationss. We show in each case the lateral view, the isolated view of the inclusions and the cross section at z = 0 mm. The red line indicates the position of the cross section.

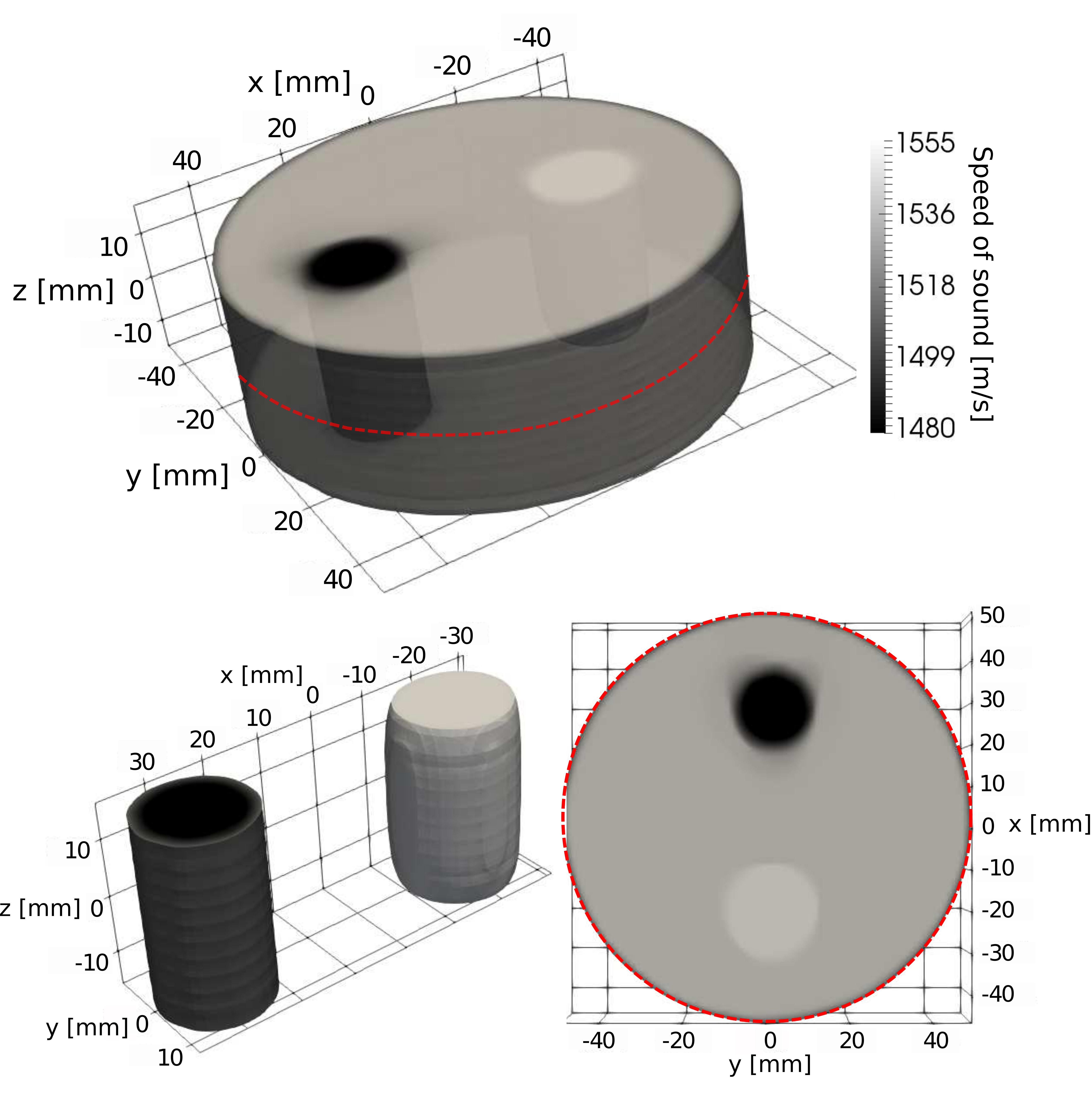
Finite-frequency tomography minimizes cross-correlation traveltime shifts between the observations and calibration data in water, being internally consistent with the standard procedure of traveltime estimations. Moreover, the availability of calibration data in water allows us to provide analytical expressions of cross-correlation traveltime sensitivity, which define our forward operator. To improve computational efficiency, we develop a memory-efficient implementation by encoding the Jacobian (forward) operator with a 1D parameterization. This parameterization is independent of the emitter-receiver geometry and allows us to efficiently extend the method to large-scale domains using massively parallelized operations on GPU architectures.

Cross section of the 3D sensitivity kernel (a) with and (b) without including geometrical spreading. (c) Sensitivity kernel in (b) represented as a function of distances indicated in (b) with dashed lines between the positions of the emitter \(\mathbf{x}_s\), receiver \(\mathbf{x}_r\), and an arbitrary spatial location \(\mathbf{x}\).